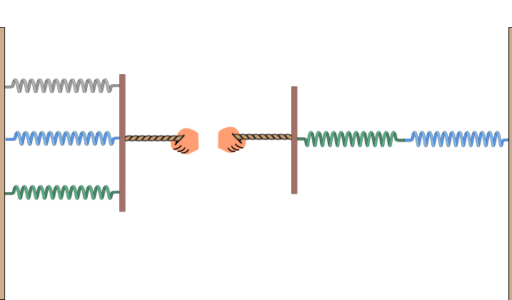
When \(n\) springs with respective constants \(k_1,k_2,\cdots ,k_n\) are connected either in series or in parallel, the whole system of springs behaves as a single one with an equivalent constant \(k\). The problem is to find \(k\) in terms of \(k_1,k_2,\cdots,k_n\).

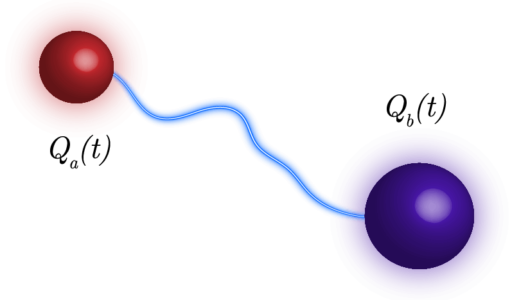
In the present post, we calculate the dependence on time of the charges on two conducting spheres connected by a wire until reaching the electrostatic equilibrium.

We were taught that grounding a conductor (by connecting it to the ground with a wire) means fixing its electric potential to zero. That’s right, but what is the physical mechanism that fixes to zero the electric potential? Let’s see how grounding a conductor works in physical terms.

When I was a student, I remember they taught me that the method of images to solve the problem of finding the electrostatic potential outside a grounded conducting sphere in the presence of an external point charge is a kind of miracle. But in physics, there are not miracles. Here are the facts why the method works

There are several problems on ballistic that illustrate in a straightforward manner the application of Newton’s equations to parabolic motion. Think for example that a projectile is launched in front of a fence of height \(h\) located at a distance \(L\) from the place of firing.

Here is an example of the application of Newton’s second law of motion to a ballistic problem. The problem we want to consider is calculating the critical angle \(\theta_c\) of firing a projectile from the ground toward a high place (of height \(h\)), located at a distance \(L\) in front of the place of firing.

Ballistic motion is one of the more elementary problems where the application of Newton’s second law is straightforward. The problem to be considered in the present article is the calculation of the critical angle \(\theta_c\) of firing a projectile of mass \(m\) with initial velocity \(v_0\), that leads to a maximum horizontal reach \(x_{\text{max}}\).

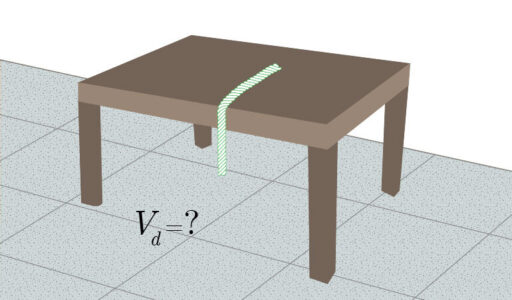
A system consisting of a rope falling down a table is considered nontrivial by many students due to the differential equation to be solved to obtain the dependence on time of the position and velocity of the rope.

Here I will take a top-to-bottom approach to introduce the theory of general relativity. Thus, I present from start the field equations. The field equations are extremely compact in the usual form that they are presented.

In this short article, I’ll give a geometric motivation for the definition of the inner product of vectors ( also called scalar product). The objects that we will be considering are arrows in the three-dimensional space and they will be represented by Latin letters.