Springs connected in series and in parallel

When \(n\) springs with respective constants \(k_1,k_2,\cdots ,k_n\) are connected either in series or in parallel, the whole system of springs behaves as a single one with an equivalent constant \(k\). The problem is to find \(k\) in terms of \(k_1,k_2,\cdots,k_n\).

Springs connected in parallel

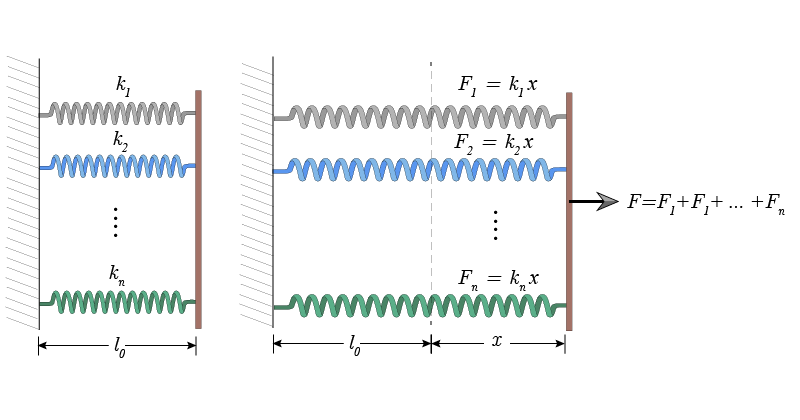
When several springs are connected in parallel, the necessary force to deform them, simultaneously and by the same amount, is the sum of the necessary force to achieve the same amount of deformation for each one of them separately. The total force on \(n\) springs is \(F=F_1+F_2+\cdots+F_n\) and the force on each spring is \(F_i=k_ix\). We omit the minus sign in the expression of the force because the force that we apply is of equal magnitude and opposite direction of the force exerted by the spring. The whole system of springs behaves as a single spring with constant \(k\) such that the total force necessary to deform it by the same amount \(x\) is \(F=kx\). Therefore we have

\begin{equation}
kx=k_1x+k_2x+\cdots+k_nx\ ,
\end{equation}

and the equivalent constant is

\begin{equation}
k=k_1+k_2+\cdots+k_n\ .
\end{equation}

Springs connected in series

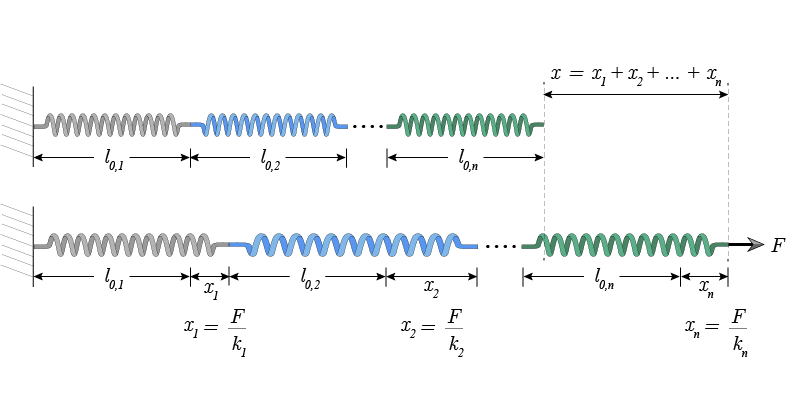
If \(n\) springs with respective constants \(k_1, k_2,\cdots ,k_n\) are connected in series and an external force \(F\) is applied, the force exerted on each one of the springs is the same. Each spring will be deformed by an amount equal to the force divided by the spring constant \(x_i=F/k_i\) for \(i=1,2,\cdots ,n\). The total deformation is \(x=x_1+x_2+\cdots+x_n\) and therefore

\begin{equation}
\frac{F}{k}=\frac{F}{k_1}+\frac{F}{k_2}+\cdots+\frac{F}{k_n}\ ,
\end{equation}

so that the equivalent spring constant is

\begin{equation}
\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\cdots+\frac{1}{k_n}\ .
\end{equation}

Example: Springs connected in series-parallel

As an illustration, let’s calculate the spring constant equivalent to a set of three springs connected in parallel that are in turn connected in series to another set of two springs connected in parallel.

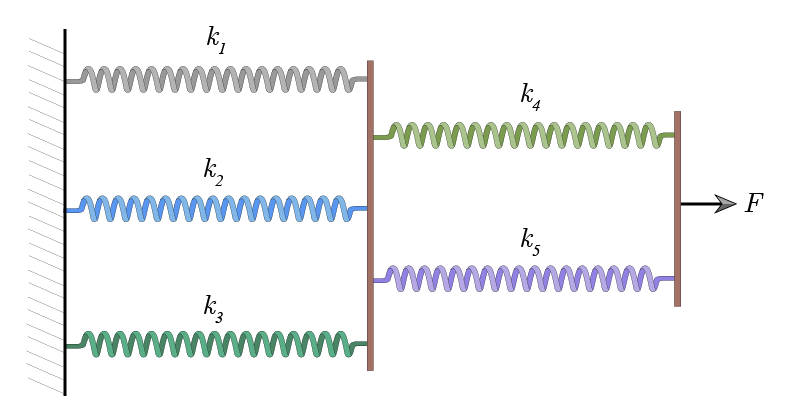
The equivalent constant \(k\) in this example is just

\begin{equation}
\frac{1}{k}=\frac{1}{k_1+k_2+k_3}+\frac{1}{k_4+k_5}\ .
\end{equation}