CHAPTER 1.
Static electric fields

Coulomb’s law

Coulomb’s law is the force law between static point charges in the vacuum. It says that the magnitude of the force between two static point charges is proportional to the magnitude of the charges and is inversely proportional to the square of the distance between them. The direction of the force is along the line connecting the charges. The force is of attraction for dissimilar charges and of repulsion for similar ones.
According with Coulomb’s law, the electric force \(\vec{F}\) on the charge \(q_1\) located at \(\vec{r}_1\), due to the charge \(q_2\) located at \(\vec{r}_2\)is
\begin{equation}
\vec{F}=k\frac{q_1q_2}{\left|\vec{r}_1-\vec{r}_2\right|^2}\frac{\vec{r}_1-\vec{r}_2}{\left|\vec{r}_1-\vec{r}_2\right|}\ ,
\end{equation}
where \(k\) is a constant.

We consider the SI system of units. In the SI system, the electric charge is measured in Coulomb (C). In SI units, the constant takes the value \(k=9.99\times10^9Nm^2/C^2\). This constant is related to another one called the dielectric permittivity of the vacuum \(\varepsilon_0= 8.8541878128(13)\times10^{−12} C^2/Nm^2\). The two constants are related through \(k=(4\pi\varepsilon_0)^{-1}\).
It is important to emphasize that Coulomb’s law is exact for static electric charges only. For charges in motion at low speeds compared with the speed of light, the law is an approximation. The law fails for charges at relativistic velocities. The correct description of the interaction between moving charges requires the introduction of the electromagnetic field.
It is also important to emphasize that the law is valid in the vacuum only and is a good approximation in media that in a certain sense behaves like the vacuum from the electrostatic point of view. The reason is that most of the materials get polarized by the electric field of the charges, and the polarized material modifies the total force.
Electric forces between static distribution of charges are better calculated with the help of the electric field.

Electric field

The force that a given static distribution of charges exerts on a specified point charge \(q\) follows the superposition rule i.e., each point charge in the distribution exerts its force on \(q\), and the total force is the vector superposition of the individual ones. Thus, the total electric force on the point charge \(q\) located at \(\vec{r}\), due to the discrete set of charges \(q_i\) located at their respective positions \(\vec{r}_i\), is given by
\begin{equation}
\vec{F}(\vec{r})=kq\sum_{i}q_i\frac{\vec{r}-\vec{r}_i}{\left|\vec{r}-\vec{r}_i\right|^3}\ .
\end{equation}
If the charges are continuously distributed, then we can consider the continuous distribution as a discrete one composed of infinitesimal charges \(dq^{\prime}\), located at the position \(\vec{r}^{\ \prime}\), and then substitute the sum by an integral:
\begin{equation}
\vec{F}(\vec{r})=kq\int dq^{\prime}\frac{\vec{r}-\vec{r}^{\ \prime}}{\left|\vec{r}-\vec{r}^{\ \prime}\right|^3}\ .
\end{equation}
We see that in the calculation of the force, the only roll of the point charge \(q\) was to be present at the position \(\vec{r}\). Therefore we can writhe
\begin{equation}
\vec{F}(\vec{r})=q\vec{E}(\vec{r})\ ,
\end{equation}
where
\begin{equation}\label{efield}
\vec{E}(\vec{r})=k\int dq^{\prime}\frac{\vec{r}-\vec{r}^{\ \prime}}{\left|\vec{r}-\vec{r}^{\ \prime}\right|^3}
\end{equation}
is the electric field induced by the charge distribution.
The expression for the differential of charge \(dq^{\prime}\) depends on the distribution of charges. The charge distribution can be either three-dimensional or two-dimensional or one-dimensional, with respective charge densities \(\rho(\vec{r}^{\ \prime})\), \(\sigma(\vec{r}^{\ \prime})\), \(\lambda(\vec{r}^{\ \prime})\). The expression for \(dq^{\prime}\) in the respective case is
\[dq^{\prime}=\begin{cases}\rho(\vec{r}^{\ \prime})\ dvol^{\prime}\\ \sigma(\vec{r}^{\ \prime})\ da^{\prime}\\ \lambda(\vec{r}^{\ \prime})\ dl^{\prime}\end{cases}\]
Notice that in Eq.\eqref{efield} there is an integral for each of the three components of the electric field. Each integral can be single, double, or triple depending on the charge distribution being either one, two, or three dimensional respectively.
Equation \eqref{efield} is the only resource we have at this moment to calculate electric fields induced by a given stationary distribution of charges. Most of the electrostatics consists of rewriting \eqref{efield} in different equivalent ways that allow the introduction of new concepts and techniques of calculation. The new techniques exploit known mathematical tools and/or geometric symmetries when they exist, to simplify the calculations. We will emphasize this point all along the course.

The electric field of a point charge

The electric field of a point charge located at the origin of coordinates is given by
\begin{equation}
\vec{E}(\vec{r})=k\frac{q}{r^2}\hat{r}\ .
\end{equation}
Where \(\hat{r}\) is a unit vector in the radial direction. We see that \(\vec{E}\) points radially outward when \(q>0\) and radially inward when \(q<0\). The magnitude of the field, represented by the length of the vector \(\vec{E}\), is constant over the surface of any sphere whose center coincides with the charge location. The magnitude of the electric field decreases with the inverse of the square of the radius. In any plane passing through the point charge, the electric field looks as shown in the following figure.

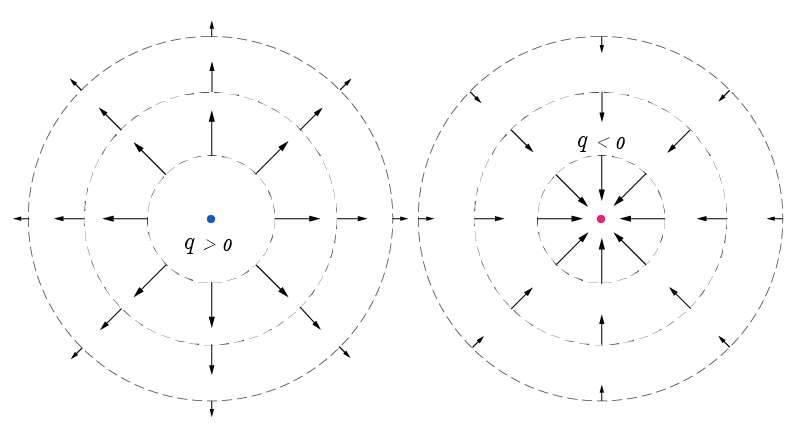
Field lines

A field line is a curve such that the electric field is tangent to it at every point except at the point where the charge is located. On the point charge the field diverges, it is not defined, and therefore, it has no sense to talk about the field being tangent to the field line at that location. The field lines are oriented. This means that at each point (except at the charge itself), the line has a direction defined by the direction of the field at that point. At each point in space, the electric field has a unique direction, and therefore field lines do not intersect. That is true except at the charge itself where all the field lines meet. Consider for example the field of a single point charge. The electric field points radially and therefore the field lines are straight lines that extend from the charge to infinite. The field lines meet at the charge and diverge from or converge to it depending on whether the charge is positive or negative.

Field lines start at positive charges and either extend to infinite or end at negative charges. As an example, consider two point-charges of different signs. In a plane that contains the two charges the field lines look like shown in the figure.

The electric field of a uniformly charged spherical shell

Let’s consider a uniformly charged spherical shell of radius \(R\) with surface charge density \(\sigma\). The spherical symmetry implies that the electric field is radially directed and depends only on the distance to the center. Therefore, it is enough to calculate the electric field along a straight line that starts at the center of the sphere. We can take that line as the \(z\) axis of the Cartesian system of coordinates with the origin at the center of the sphere.

The vector \(\vec{r}^{\ \prime}\) that points to the element of area \(d\vec{a}^{\ \prime}\) is
\[\vec{r}^{\ \prime}=R\sin\theta\cos\phi\hat{x}+R\sin\theta\sin\phi\hat{y}+R\cos\theta\hat{z}\ ,\]
while the vector \(\vec{r}\) where we want to calculate the electric field is
\[\vec{r}=z\hat{z}\ .\]
Therefore, we have
\[\vec{r}-\vec{r}^{\ \prime}=-R\sin\theta\cos\phi\hat{x}-R\sin\theta\sin\phi\hat{y}+(z-R\cos\theta)\hat{z}\ ,\]
and
\[\left|\vec{r}-\vec{r}^{\ \prime}\right|=(R^2-2Rz\cos\theta +z^2)^{1/2}\ .\]
The element of charge is given by \(dq^{\prime}=\sigma da^{\prime}\) where the element of area in spherical coordinates is \(da=R^2\sin\theta d\phi d\theta\).
The three components of the electric field are
\[
E_x(0,0,z)=k\int_0^{\pi}\int_0^{2\pi}\frac{(-R\sin\theta\cos\phi)\sigma R^2\sin\theta d\phi d\theta}{(R^2-2Rz\cos\theta +z^2)^{3/2}}\ ,
\]
\[
E_y(0,0,z)=k\int_0^{\pi}\int_0^{2\pi}\frac{(-R\sin\theta\sin\phi)\sigma R^2\sin\theta d\phi d\theta}{(R^2-2Rz\cos\theta +z^2)^{3/2}}\ ,
\]
\[
E_z(0,0,z)=k\int_0^{\pi}\int_0^{2\pi}\frac{(z-R\cos\theta))\sigma R^2\sin\theta d\phi d\theta}{(R^2-2Rz\cos\theta +z^2)^{3/2}}\ .
\]
The integral with respect to \(\phi\) in the \(E_x\) and \(E_y\) components is zero. Indeed, the only term depending on \(\phi\) in both cases is just \(\cos\phi\) in \(E_x\) and \(\sin\phi\) in \(E_y\), and both integrals between \(0\) and \(2\pi\) vanish.
The integral with respect to \(\phi\) in the \(E_z\) component is just \(2\pi\) because the integrand doesn’t depend on \(\phi\). To integrate with respect to \(\theta\) we change to the variable \(u\) as follows:
\[u=R^2-2Rz\cos\theta +z^2\ ,\]
\[0\leq\theta\leq\pi\ \Rightarrow\ (R-z)^2\leq u\leq (R+z)^2\ ,\]
\[\cos\theta=\frac{R^2+z^2-u}{2Rz}\ ,\]
\[\sin\theta d\theta=\frac{du}{2Rz}\ ,\]
\[z-R\cos\theta=\frac{z^2-R^2+u}{2z}\ .\]
The integral for \(E_z\) becomes
\[E_z(0,0,z)=2\pi k\sigma R^2\int_{(R-z)^2}^{(R+z)^2}\frac{(z^2-R^2+u)}{2z\ u^{3/2}}\frac{du}{2Rz}\ ,\]
which can be rewritten in the form
\[E_z(0,0,z)=\frac{\pi k\sigma R}{2z^2}\int_{(R-z)^2}^{(R+z)^2}[(z^2-R^2)u^{-3/2}+u^{-1/2}]du\ ,\]

The integrals are easily calculated:
\[\int_{(R-z)^2}^{(R+z)^2}u^{-3/2}du=-\frac{2}{\left|R+z\right|}+\frac{2}{\left|R-z\right|}=\begin{cases}
-\frac{4R}{R^2-z^2} &; z>R \\
\frac{4z}{R^2-z^2} &; z <R\end{cases}\ ,\]
\[\int_{(R-z)^2}^{(R+z)^2}u^{-1/2}du=2\left|R+z\right|-2\left|R-z\right|=\begin{cases}4R &; z>R \\ 4z &; z<R\end{cases}\ .\]

The absolute value comes from taking the square root of the square of an expression. The final result is
\[E_z(0,0,z)=\begin{cases} k\frac{4\pi R^2\sigma}{z^2} & ; z>R \\ 0 & ; z<R\ .\end{cases}\]
We see that the electric field outside the uniformly charged spherical shell is identical to the field of a point charge of the same magnitude as the total charge on the sphere namely \(4\pi R^2\sigma\), located at the center. We will re-derive this result more easily later with the help of Gauss law.
Notice that we have calculated the electric field outside (\(z>R\)) and inside (\(z<R\)) but not on the sphere surface (\(z=R\)). Notice that the field jumps from zero inside to nonzero outside. It would be wrong to extrapolate the result for the field outside the sphere to get the field exactly on the sphere surface. The correct calculation is as follows. Take the integral expression for the field
\[E_z(0,0,z)=\frac{\pi k\sigma R}{2z^2}\int_{(R-z)^2}^{(R+z)^2}[(z^2-R^2)u^{-3/2}+u^{-1/2}]du\ ,\]
and put \(z=R\) to get
\[E_z(0,0,R)=\frac{\pi k\sigma R}{2R^2}\int_{0}^{4R^2}u^{-1/2}du\ .\]
The result is
\[E_z(0,0,R)=k\frac{4\pi R^2 \sigma }{2R^2} .\]
We have not simplified the final result to indicate that it is just half of the limit \(\left. E_z\right|_{z\to R^+}\). More precisely, the electric field on the surface of the sphere is the average between the field just inside and just outside the sphere, where “just” means here very close to the surface.

The electric field of a uniformly charged ball

Let’s consider a uniformly charged ball of radius \(R\) and charge density \(\rho\). The electric field can depend on the radial distance from the center only and is radially directed. We can consider the ball as consisting of a set of uniformly charged spherical shells of thickness \(dr\). The total charge \(dq\) in a shell of radius \(r\) is the density \(\rho\) times the volume \(4\pi r^{2}dr\) of the shell:
\[dq=\rho4\pi r^{2}dr\]
For a shell of radius \(0\leq r\leq R\), we know that the contribution \(dE_z(0,0,z)\) to the electric field for \(z>r\) is
\[dE_z(0,0,z)=k\frac{4\pi r^{2}\rho dr}{z^2}\ .\]
Let’s consider the case \(z>R\) first. In this case the point \((0,0,z)\) is outside of all the shells. Therefore we just have to add the contributions of all the shells for \(0\leq r\leq R\) to get
\begin{align*}
E_z(0,0,z)&=k\int_0^R\frac{4\pi r^{2}\rho dr}{z^2}\\
&=k\frac{(4/3)\pi R^3\rho}{z^2}\ .
\end{align*}
Now consider the case \(0<z<R\). Notice that the contribution to the electric field at \(0<z<R\) coming from the shells in the region \(z<r<R\) is zero. Indeed, the point \((0,0,z)\) is inside all those shells, and we saw that the electric field inside a uniformly charged spherical shell is zero.
The only nonzero contribution to the electric field comes from all the shells contained in the region \(0\leq r\leq z\), and therefore
\begin{align*}
E_z(0,0,z)&=k\int_0^z\frac{4\pi r^{2}\rho dr}{z^2}\\
&=k\frac{(4/3)\pi z^3\rho}{z^2}\\
&=k\frac{4\pi\rho z}{3}\ .
\end{align*}
We see that inside the ball, the electric field increases linearly with the distance to the center, while outside it behaves as the field of a point charge at the center.
In this case, the electric field is continuous at \(z=R\). Notice that there is no surface density of charge in this case. Indeed, the charge is uniformly distributed along the volume, and any two-dimensional surface has zero volume and therefore zero electric charge. That is why we considered spherical shells with thick \(dr\).

The electric field of a uniformly charged infinite plane

Let’s consider an infinite plane uniformly charged with charge density \(\sigma\). Due to the planar symmetry of the problem, the electric field cannot depend on the location parallel to the plane. It can depend on the distance from the plane only. We can take the \(z\) axis perpendicular to the plane and make the plane to coincide with the \(xy\)-plane. It is enough to calculate the electric field along the \(z\) axis. To this end, it is easier to use polar coordinates on the plane.

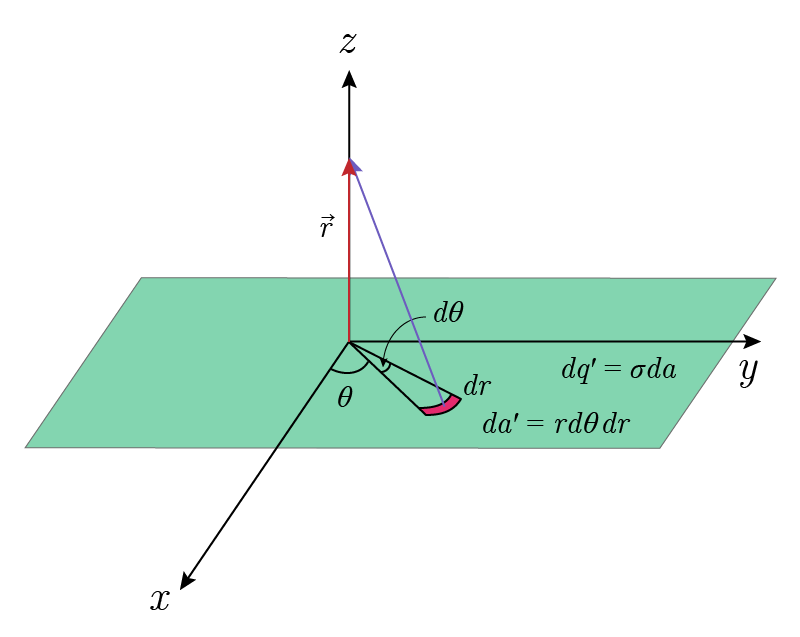
\[\begin{cases}\vec{r}=z\hat{z} \\ \vec{r}^{\ \prime}=r\cos\theta\hat{x}+r\sin\theta\hat{y} \\ dq^{\prime}=\sigma rd\theta dr\end{cases}\]
Therefore we have
\[\begin{cases}\vec{r}-\vec{r}^{\ \prime}=-r\cos\theta\hat{x}-r\sin\theta\hat{y}+z\hat{z} \\
|\vec{r}-\vec{r}^{\ \prime}|=(r^2+z^2)^{1/2}\end{cases}\]
The electric field is given by Eq.\eqref{efield}. Its components are
\[E_{x}=k\int_0^{\infty}\int_0^{2\pi}\frac{\sigma rd\theta dr (-r\cos\theta)}{(r^2+z^2)^{3/2}}=0\]
\[E_{y}=k\int_0^{\infty}\int_0^{2\pi}\frac{\sigma rd\theta dr (-r\sin\theta)}{(r^2+z^2)^{3/2}}=0\]
\[E_{z}=k\int_0^{\infty}\int_0^{2\pi}\frac{\sigma rd\theta dr z}{(r^2+z^2)^{3/2}}\]
The components of the electric field parallel to the plane are both zero. This can be concluded either from the direct calculation of the respective integrals or from the symmetry of the problem.
In the \(z\) component of the field, the integral with respect to the angle gives just a factor of \(2\pi\), reducing the calculation to
\[E_{z}=2\pi k\sigma z\int_0^{\infty}\frac{rdr}{(r^2+z^2)^{3/2}}=2\pi k\sigma\frac{z}{|z|}\]
The absolute value \(|z|\) in the denominator comes from \(\sqrt{z^2}\). The ratio \(z/|z|\) is \(+1\) for \(z>0\) and \(-1\) for \(z<0\). Remember that the constant \(k\) is related to the constant \(\varepsilon_0\) through \(4\pi k=1/\varepsilon_0\). Therefore, the electric field of the infinite plane is \[\vec{E}=\begin{cases}\ \ \frac{\sigma}{2\varepsilon_0}\hat{z} & \text{for}\ z>0\\-\frac{\sigma}{2\varepsilon_0}\hat{z} & \text{for}\ z<0\end{cases}\]
We conclude that the electric field of the uniformly charged infinite plane is constant on both sides, perpendicular to the plane, and discontinuous at the plane.