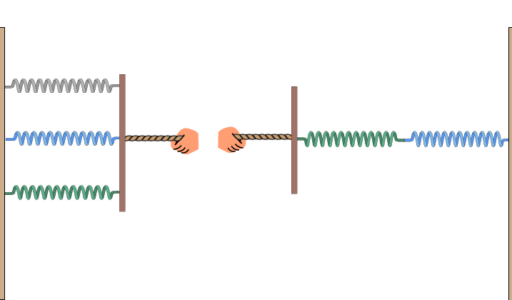
When \(n\) springs with respective constants \(k_1,k_2,\cdots ,k_n\) are connected either in series or in parallel, the whole system of springs behaves as a single one with an equivalent constant \(k\). The problem is to find \(k\) in terms of \(k_1,k_2,\cdots,k_n\).
There are several problems on ballistic that illustrate in a straightforward manner the application of Newton’s equations to parabolic motion. Think for example that a projectile is launched in front of a fence of height \(h\) located at a distance \(L\) from the place of firing.
Here is an example of the application of Newton’s second law of motion to a ballistic problem. The problem we want to consider is calculating the critical angle \(\theta_c\) of firing a projectile from the ground toward a high place (of height \(h\)), located at a distance \(L\) in front of the place of firing.
Ballistic motion is one of the more elementary problems where the application of Newton’s second law is straightforward. The problem to be considered in the present article is the calculation of the critical angle \(\theta_c\) of firing a projectile of mass \(m\) with initial velocity \(v_0\), that leads to a maximum horizontal reach \(x_{\text{max}}\).
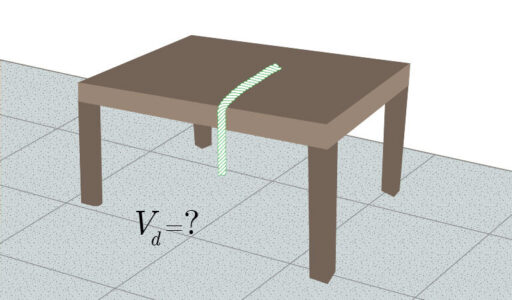
A system consisting of a rope falling down a table is considered nontrivial by many students due to the differential equation to be solved to obtain the dependence on time of the position and velocity of the rope.
In this short article, I’ll give a geometric motivation for the definition of the inner product of vectors ( also called scalar product). The objects that we will be considering are arrows in the three-dimensional space and they will be represented by Latin letters.
The moment of inertia of a rigid body is clearly defined and explicit calculations for a thin rod or stick, a cylindrical shell and a disk, are made.
The one-dimensional simple harmonic oscillator is described by the differential equation \begin{equation} m\frac{d^2x}{dt^2}+kx=0 \end{equation} Here \(m\) is the mass of the particle and \(k\) is the constant characterizing the restoring force. Solution of the simple harmonic oscillator The solution satisfying the initial condition \(x(0)=A\), where \(A\) is the amplitude of the oscillations, is given by