The equation \(E=Mc^2\) is probably one of the most famous equations in the history of physics, and its meaning has been amply discussed. However, it is common that people don’t know how Einstein got this beautiful result. In the present post I will show you a derivation of this equation. The derivation is actually simple and is based on the principle of relativity. This is not exactly the original derivation, but a simpler one attributed to Einstein also. Before we start, it is necessary to say some words about the principle of relativity and about electromagnetic waves. Those are the ingredients for obtaining the famous formula.
The principle of relativity of the special relativity establishes that the physical laws are valid and take the same form in all inertial reference system. In our case, we will consider the laws of energy and momentum conservation, and the laws governing the propagation of electromagnetic waves.
I want to clarify that there is a principle of relativity in non relativistic physics. This principle establishes that the laws of mechanics are valid and take the same form in all inertial reference frame. Einstein generalized this principle to include not only the laws of mechanics, but all of the laws of physics. This could sound trivial, but actually has important consequences. One of these consequences is the equivalence of mass and energy as we will see.
From the Maxwell’s equations, one can infer the existence of electromagnetic waves that in vacuum propagate at the constant speed \(c\). The Maxwell’s equations take exactly the same form in all inertial reference system, and therefore, the speed of light has to be the same in all of them. The only thing that can change from one reference frame to another, is the direction of propagation of the electromagnetic wave, but its speed is the same.
Maxwell’s equations imply that electromagnetic waves carry linear momentum. This was a surprising result amply confirmed by meticulous experiments. Electromagnetic waves do not posses mass, and therefore, the linear momentum cannot be defined as is done for material bodies, i.e., cannot be defined as \(\vec{p}=m\vec{v}\). Maxwell’s theory gives the correct expression for the linear momentum carried by an electromagnetic wave, not in term of mass, but in terms of energy. The magnitude of the linear momentum of an electromagnetic wave of energy \(E\) is given by \(p=E/c\) (The direction of the linear momentum vector is given by the Pointing’s vector, I will talk about this in another post).
Now we are ready to derive the mass-energy equivalence. The equation is consequence of the principle of relativity, and therefore, we will need to consider two different inertial reference frames. One of them, will be the rest frame of a body \(A\) whose rest mass is \(M\).
Absorption of energy as seen in the rest frame of the body
Consider a body \(A\) at rest in the reference frame \(S\). The body’s mass in this reference frame is \(M\). This is called rest mass of the body and is commonly denoted \(m_0\). Now let’s suppose that two pulses of radiation, each one of energy \(E/2\), and traveling parallel to the \(y\) axis in opposite directions, are incident on the body and are completely absorbed by it (see the figure below).
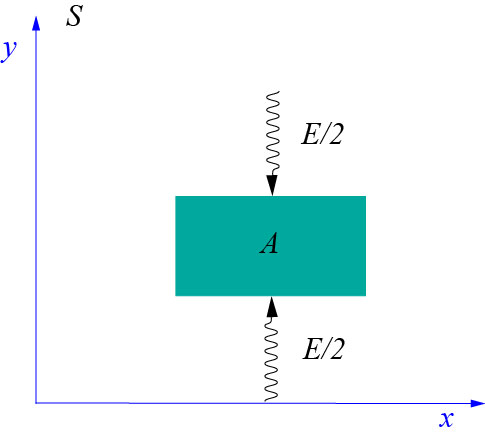
The law of the conservation of energy implies that the energy of the body had to increase by the amount \(E\). It is also clear from the symmetry of the configuration, that the body will remain at rest in \(S\) after absorbing the two pulses of radiation. This last statement is simply the law of conservation of the linear momentum.
At this point we don’t know whether the mass of the body was affected in some way by the absorbed energy. To emphasize this, we will use the symbol \(\tilde{M}\) to designate the mass of the body after it has absorbed the radiation.
Our task is to find the relation between the mass \(M\) before the absorption, The absorbed energy \(E\) and the mass \(\tilde{M}\) after the absorption has taken place. For this end, it is necessary to look at this process from a second inertial reference frame.
The absorption process as seen from a traveling inertial reference frame
Let’s call \(S^{\prime}\) to a second reference frame which is traveling at constant velocity \(v\) in the negative direction of the \(x\) axis (see the figure).
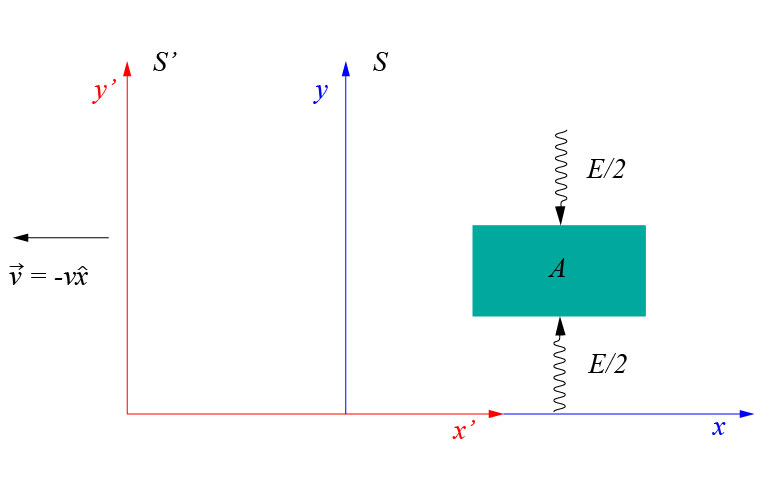
From the point of view of this reference frame, the body is traveling in the positive direction of the \(x\) axis at velocity \(\vec{u}=v\hat{x}\). In addition, the pulses of radiation travel forming an angle \(\alpha\) with the vertical in this frame of reference (see the figure).
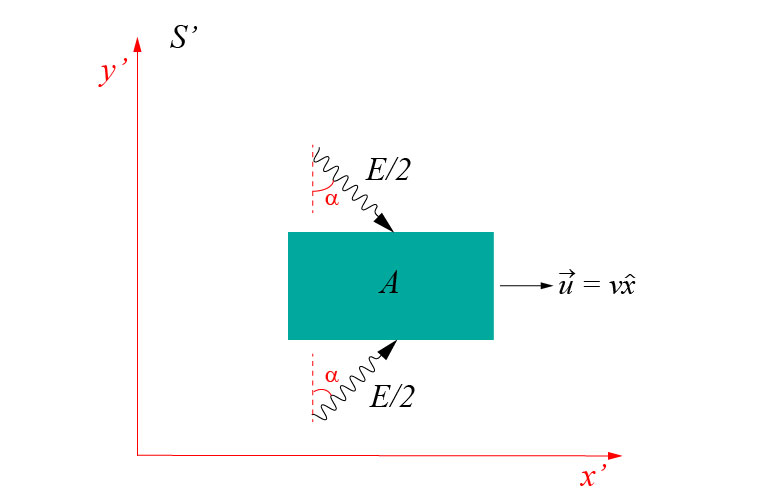
In this section we will consider the case when the magnitude \(v\) of the velocity is very small compared with the speed of light \(c\). This consideration allows us to put \(\gamma=1\) with good approximation, and thus we do not have to deal with Lorentz transformations. Later we will see that the full treatment, considering Lorentz transformations, leads to exactly the same result.
What we want to do, is to use the law of conservation of momentum in this frame. It will suffice to consider the momentum conservation law in the \(x\) direction. For this end, let’s calculate the total momentum (in the \(x\) direction) of the system (body plus radiation) before and after the radiation is absorbed by the body.
Before the absorption, the body has mass \(M\) and velocity \(v\) in the positive direction of the \(x\) axis. Therefore its momentum is \(Mv\).
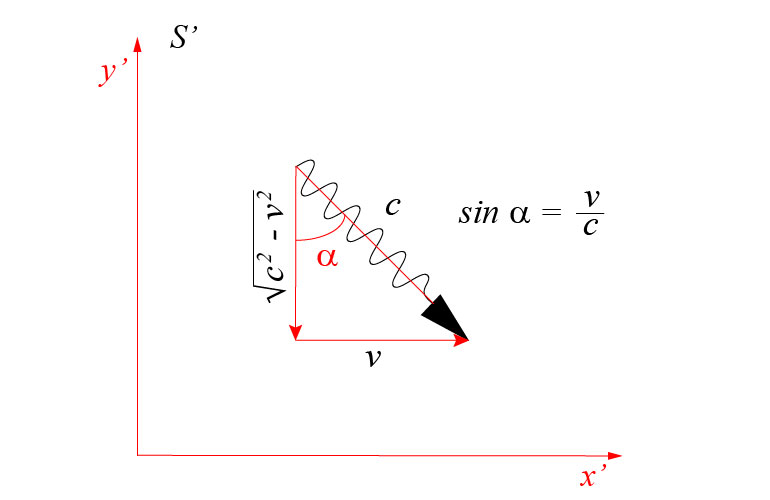
In this reference frame, the radiation has components of momentum in both, the \(x\) and the \(y\) directions. The component of the momentum of each pulse of radiation in the \(x\) direction is \((E/2c)\sin\alpha\) . The value of \(\sin\alpha\) is clearly seen to be \(\sin\alpha=v/c\) (see the figure below). Therefore, the total momentum in the \(x\) direction is:
\[p_{x,\text{before}}=Mv+2\cdot\frac{E}{2c}\cdot\frac{v}{c}\]
Let’s note that after the absorption of the radiation, the body doesn’t change its velocity because it still remains at rest in \(S\) (remember that the velocity of the body in \(S^{\prime}\) to the right, is simply due to the relative motion of the reference system \(S^{\prime}\) to the left while \(A\) remains at rest in \(S\)). Therefore, after the absorption has taken place, the total momentum is
\[p_{x,\text{after}}=\tilde{M}v\]
Conservation of momentum implies the equality of the total momentum before and after the absorption:
\[Mv+2\cdot\frac{E}{2c}\cdot\frac{v}{c}=\tilde{M}v\]
We see that the last relation implies that, after absorbing the amount of energy \(E\), the body’s rest mass increases by an amount \(E/c^2\), i.e.:
\[\Delta M=\tilde{M}-M=\frac{E}{c^2}\]
This means that adding the amount of energy \(E\) to the body \(A\), while it remains at rest, increases the inertia of \(A\) (at rest) by an amount equivalent to the inertia of another body whose rest mass is numerically equivalent to the quantity \(E/c^2\). Notice that what increases is the inertia of the body, not its amount of matter. Mass is a measure of inertia, not an indicative of amount of substance.
The inertia of a body is a measure of its resistance to changes in its state of motion. If the same force is applied to two different bodies, the body that experiences less changes in its motion, possesses more inertia than the other one. this inertia is quantified by the inertial mass.
A possible misconception
The discussion in the precedent section could lead us to think that one pulse of radiation, whose energy is \(E\), could be considered as a particle of mass \(m_0=E/c^2\) traveling at the speed of light \(c\), and therefore its linear momentum would be \(p=m_0c=E/c\), which is the energy momentum relation that the electromagnetic theory predicts! But, we have to be careful. Electromagnetic radiation propagates as waves, not as particles. The corpuscular behavior of the radiation manifests itself in interaction with matter, but during propagation, electromagnetic radiation still behaves as waves. In addition, material particles cannot travel at the speed of light and therefore, it is not correct to interpret the result as assigning a mass \(m_0=E/c^2\) to a pulse of radiation of energy \(E\). Indeed, the rest mass of light is zero.
What happens if the reference frame \(S^{\prime}\) has a relative velocity comparable to the speed of light?
If the reference frame \(S^{\prime}\) has a large velocity comparable to the speed of light, we cannot assert that the total energy \(E\) of the radiation measured in \(S\), will take the same value in \(S^{\prime}\). Indeed, the right thing to do, is to designate the total energy of the pulses as \(E^{\prime}\) when measured in \(S^{\prime}\). The relation between the two, is given by the energy-momentum Lorentz transformation. In the specific case we are considering, the transformation of the total energy between the two reference systems is simply \(E^{\prime}=\gamma E\). This implies that the \(x\)-component of the total momentum of the radiation measured in \(S^{\prime}\) is
\[p_{x, \text{rad, before}}^{\prime}=2\cdot\frac{\gamma E}{2c}\cdot\frac{v}{c}\]
What about the body \(A\)? Well, the rest mass of the body before and after the absorption of the radiation is \(M\) and \(\tilde{M}\) respectively. In the reference frame \(S^{\prime}\), the body has a velocity whose magnitude is \(v\). Therefore, the inertial masses \(M^{\prime}\), and \(\tilde{M}^{\prime}\) of \(A\) in \(S^{\prime}\), before and after the absorption, are respectively
\begin{align*}
M^{\prime}&=\gamma M\\
\tilde{M}^{\prime}&=\gamma\tilde{M}
\end{align*}
This means that the momentum balance in the \(x\) direction in \(S^{\prime}\) is
\[\gamma Mv+2\cdot\frac{\gamma E}{2c}\cdot\frac{v}{c}=\tilde{\gamma M}v\]
which, evidently is equivalent to the equation obtained in the last section above. The only difference is a factor of \(\gamma\) in each term of the equation, which obviously can be canceled.
I will talk about the meaning, and the consequences of this equivalence in another post.

Leave a comment