In the present, and in other posts, I will show you how to apply the Gauss law to calculate the electric field of several charge distributions.
I will start with some conventional problems which are relatively easy, and after that, I will consider more advanced problems. I will show you how to solve some problems that seem to be challenging. The difficulty in solving that kind of problems is frequently due to a lack of true understanding of the involved concepts.
I will explain in detail a relatively large amount of problems. I will do that through several post.
Before we start solving problems, it is convenient to recall some key concepts. If you are familiarized with these concepts, you can jump directly to the examples. If one problem seems easy for you, try another one. I’m sure you will find some you would not know how to solve.
The Gauss law
Let’s remember the integral form of the Gauss law:
\[\oint \vec{E}\cdot\vec{da}=\frac{Q_{enc}}{\epsilon_0}\]
Here, \(Q_{enc}\) is the net charge enclosed by the Gaussian surface. The Gauss law is always true, but it is useful only if the following two conditions are fulfilled:
- The electric field has constant magnitude on the Gaussian surface.
- The electric field is parallel to the normal vector at each point on the Gaussian surface.
If these two conditions are fulfilled, then the surface integral in the Gauss law can be simply calculated:
\[\oint\vec{E}\cdot\vec{da}=E\ A\]
where \(E=|\vec{E}|\) is the magnitude of the electric field on the Gaussian surface, and \(A\) is the area of the Gaussian surface.
We see that the magnitude of the electric field is then easily calculated:
\[E=\frac{Q_{enc}}{\epsilon_0 A}\]
Some remarks about the Gauss law
- In the Gauss law, the enclosed charge \(Q_{enc}\) has to be completely inside the Gaussian surface. Any part of the charge distribution located just at the Gaussian surface doesn’t contribute to \(Q_{enc}\).
- The charge left outside the Gaussian surface doesn’t contribute to the electric field at the Gaussian surface, but it has to be symmetrically distributed with respect to it any way. If this were not the case, we could not assure that the electric field fulfill the two conditions given in the previous section, and the calculation of the surface integral would not be so simple.
- When dielectrics are present, the Gauss law takes a slightly different form:\[\oint\vec{D}\cdot\vec{da}=Q_{f,enc}\]Here \(\vec{D}\) is the electric displacement vector, and \(Q_{f,enc}\) is the free charge enclosed by the Gaussian surface. I will talk about this in another post.
In order to be able to solve nontrivial problems, it is necessary to pay attention to some properties of conductors and insulators
Conductors and insulators
In an insulator we can spread some electric charge all along the insulator volume. The charges will remain at the place they were located because an electric field cannot displace them (unless the electric field is strong enough).
Conductors have the following properties:
- The electric field inside the conductor’s body is always zero.
- The net charge density inside the conductor’s body is always zero.
- Any net charge resides on the conductor’s surface .
- The electric field on the conductor’s surface is always perpendicular to the surface and pointing outward.
- The electric potential is always constant all along the body and surface of the conductor. This is so because the electric field is zero inside, and the electric field is the gradient of the potential.
Now we are ready to start solving problems.
The electric field of a uniformly charged spherical shell
The problem is to calculate the electric field due to a charged spherical shell of radius \(R\) which has an evenly distributed net charge \(Q\).
This is the simplest of all the problems (or the second one, if one consider also the problem of calculating the electric field of a point charge, which is really trivial). Its solution follows immediately from the Gauss law.
If we take a Gaussian surface of radius \(r\) which is concentric with the shell, then the enclosed charge \(Q_{enc}\) will be zero for \(r<R\), and will be the net charge \(Q\) of the shell for \(r>R\). In addition, the electric field is radially directed due to the spherical symmetry. The area of the Gaussian surface is \(A=4\pi r^2\). Therefore, the electric field is:
\[\vec{E}\left(\vec{r}\right)=\begin{cases}
\vec{0}, & \text{ for $r<R$}\\
\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\hat{r}, & \text{ for $r>R$},
\end{cases}\]
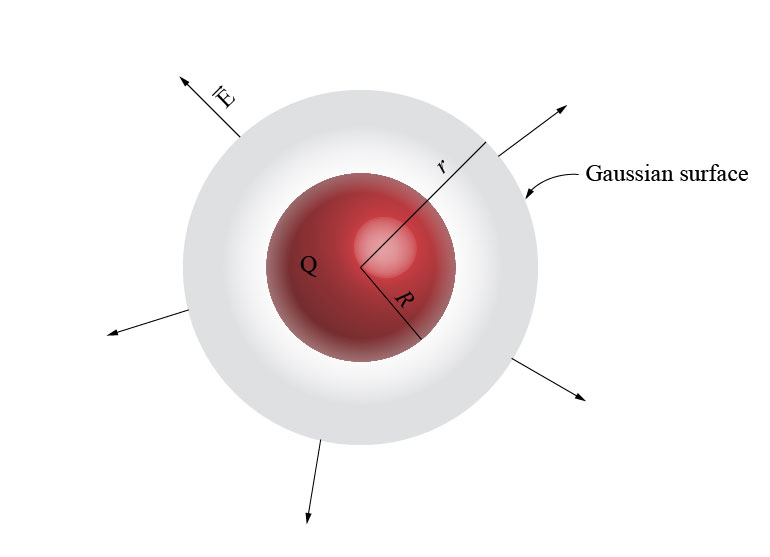
Let’s note that the electric field just at the shell, i.e., at \(r=R\), cannot be calculated by using the Gauss law (see the remarks about the Gauss law). In that case we will need to use directly the definition of electric field and calculate the corresponding integral. I will show you how to calculate it in another post. In the mean time, I can tell you that the electric field at \(r=R\) is the average of the electric field just inside and just outside the shell.
The component of the electric field in the direction of the normal vector to a charged surface (a two-dimensional layer of charge) is always discontinuous at the surface. We cannot use the Gauss law to calculate the electric field just at the surface, but we can use it to calculate the “jump” in the normal component of the field when passing from one side of the surface to the other side (I explain how to do that in the following post).
The electric field of a uniformly charged ball
The problem is to calculate the electric field due to a charged ball of radius \(R\) which has an evenly distributed net charge \(Q\).
In order to calculate the electric field, we simply take a spherical Gaussian surface just as we did in the case of a spherical shell. It is clear that the field depends on the net charge enclosed, but not on the precise way it is distributed, as long as the distribution is spherically symmetric.
This implies that the enclosed charge can be evenly spread on either a spherical shell, or a ball, or be concentrated in a point at the center of the Gaussian surface. All these configurations of charge will produce the same electric field.
Therefore , for \(r>R\) the field is given by
\[\vec{E}\left(\vec{r}\right)=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\ \hat{r}\]
For \(r<R\) we simply have to calculate the amount of charge enclosed by the spherical Gaussian surface of radius \(r\) (the charge in the outside of the Gaussian surface doesn’t contribute to the electric field on the Gaussian surface). Clearly, in this case \(Q_{enc}<Q\). How do we calculate \(Q_{enc}\)? Well, If we know the density \(\rho\) of the distribution of charge, all what we need to do is to integrate it in the respective volume:
\[Q_{enc}=\int\rho dV\]
In the present case, the density is constant and equal to the total charge \(Q\) divided by the volume of the ball \(4\pi R^3/3\):
\[\rho=\frac{3Q}{4\pi R^3}\]
Therefore, the enclosed charge is
\[Q_{enc}=\rho\int dV\]
We could put \(\rho\) outside of the integral because it is constant.
Now we have to calculate the integral, but this is a trivial task. It is just the volume of a ball of radius \(r<R\), namely, \(4\pi r^3/3\). Thus, the enclosed charge is
\[Q_{enc}=\left(\frac{3Q}{4\pi R^3}\right)\left(\frac{4\pi r^3}{3}\right)=\left(\frac{r}{R}\right)^3Q\]
The area of the Gaussian surface is \(A=4\pi r^2\), and the electric field is radially directed. Therefore, for \(r<R\) the electric field is:
\[\vec{E}\left(\vec{r}\right)=\frac{Q\left(r^3/R^3\right)}{4\pi\epsilon_0 r^2}\hat{r}=\frac{Qr}{4\pi\epsilon_0R^3}\ \hat{r}\]
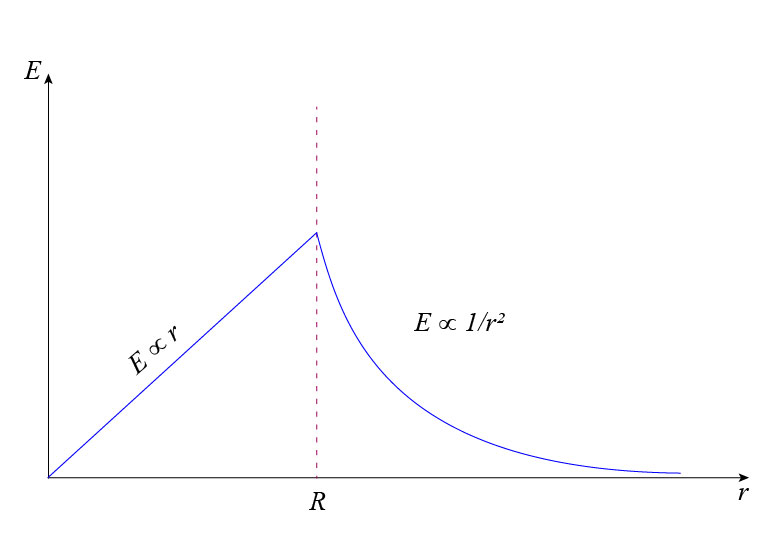
We can summarize the results as follows:
\[\vec{E}=\begin{cases}
\frac{Qr}{4\pi\epsilon_0R^3}\ \hat{r}, & \text{for $0\leq r\leq R$}\\
\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\ \hat{r}, & \text{for $r\geq R$}
\end{cases}\]
In this case the electric field is continuous at \(r=R\). You can check it by noting that the last expression takes at \(r=R\) a consistent value.
The magnitude of the electric field increases linearly inside the ball, i.e., for \(0\leq r\leq R\), and after that, decreases as \(1/r^2\) for \(r\geq R\).
I have to say some words about the results obtained in the present section. We have implicitly assumed that the insulator in which the charges are evenly distributed, has negligible electric susceptibility. In other words, we assumed that polarization effects and the polarization field are negligible. I will explain more about this in another post.

Leave a comment