What is an electric dipole?
An electric dipole is a pair of electric charges of equal magnitude \(q\) and opposite sign separated a small distance \(d\).

The vector that points from the negative to the positive charge, and whose magnitude is the product of the positive charge \(q\), times the distance of separation \(d\), is called moment of dipole \(\vec{p}\).
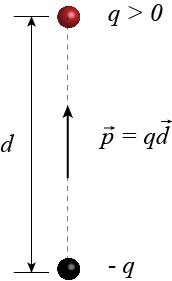
Potential of the electric dipole
The distance \(r\) from the electric dipole is measured from the middle point between the charges. At any distance \(r\) from the electric dipole, the potential of the electric dipole \(\Phi\) is given by the sum of the electric potential of each charge.
\begin{equation}
\Phi(\vec{r})=\frac{1}{4\pi\epsilon_0}\left[\frac{q}{r_+}+\frac{-q}{r_{-}}\right]
\end{equation}
For a given distance \(r\) from the dipole the electric dipole potential varies with the angle \(\theta\) between the vectors \(\vec{p}\) and \(\vec{r}\).
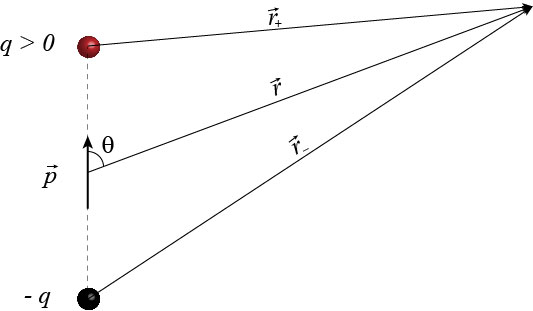
The distances \(r_+\), and \(r_-\) can be calculated in terms of the distance \(r\) from the dipole, the separation \(d\) between the charges, and the angle \(\theta\). For this end we use the law of cosines for a triangle with sides \(r\), \(d/2\), and either \(r_+\) and opposite angle \(\theta\), or \(r_-\) and opposite angle \(180^o-\theta\):
\[r_+=\left[r^2-2r\frac{d}{2}\cos\theta+\left(\frac{d}{2}\right)^2\right]^{1/2}\]
\[r_{-}=\left[r^2+2r\frac{d}{2}\cos\theta+\left(\frac{d}{2}\right)^2\right]^{1/2}\]
In the last equation we used the identity \(\cos(180^o-\theta)=-\cos\theta\).
Power expansion of the potential of the electric dipole
We can rewrite the expressions for \(1/r_+\) and \(1/r_-\) in terms of the ratio \(d/r\):
\[\frac{1}{r_+}=\frac{1}{r}\left[1-\frac{d}{r}\left(\cos\theta-\frac{1}{4}\frac{d}{r}\right)\right]^{-1/2}\]
\[\frac{1}{r_-}=\frac{1}{r}\left[1+\frac{d}{r}\left(\cos\theta+\frac{1}{4}\frac{d}{r}\right)\right]^{-1/2}\]
For distances \(r\) larger than the charge separation \(d\), we can expand the potential of each charge in terms of powers of the ratio \(d/r\). For this end we recall the binomial expansion
\[(1-x)^{\alpha}=1-\frac{\alpha}{1!}x+\frac{\alpha(\alpha-1)}{2!}x^2-\frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3\cdots\]
\[(1+x)^{\alpha}=1+\frac{\alpha}{1!}x+\frac{\alpha(\alpha-1)}{2!}x^2+\frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3\cdots\]
In our case, we have \(\alpha=-1/2\), and either \(x=(d/r)\left[\cos\theta-d/(4r)\right]\), or \(x=(d/r)\left[\cos\theta+d/(4r)\right]\). The expansion will be valid as long as \(|x|<1\). We will be interested in the case when \(d/r\ll 1\).
\[\frac{1}{r_+}=\frac{1}{r}\left\{1+\frac{1}{2}\frac{d}{r}\left(\cos\theta-\frac{1}{4}\frac{d}{r}\right)+\frac{3}{8}\left(\frac{d}{r}\right)^2\left(\cos\theta-\frac{1}{4}\frac{d}{r}\right)^2+\cdots\right\}\]
\[\frac{1}{r_-}=\frac{1}{r}\left\{1-\frac{1}{2}\frac{d}{r}\left(\cos\theta+\frac{1}{4}\frac{d}{r}\right)+\frac{3}{8}\left(\frac{d}{r}\right)^2\left(\cos\theta+\frac{1}{4}\frac{d}{r}\right)^2-\cdots\right\}\]
If we substitute the two previous equations in Eq.(1), we obtain the expansion in powers of \(d/r\) for the potential of the electric dipole.
\[\Phi(r,\theta)=\frac{q}{4\pi\epsilon_0r}\left\{\frac{d\cos\theta}{r}-\frac{3\cos\theta}{16}\left(\frac{d}{r}\right)^3+\cdots\right\}\]
The term with the lower power of \(d/r\) is called the dominant term of the power expansion. This term can be considered as the approximate value of the potential, while the remnant terms are small corrections. The smaller the ratio \(d/r\) the better the approximation given by the dominant term.
Why do we need the power expansion of the potential?
It seems that the expansion in powers of \(d/r\) of the potential of dipole is an unnecessary complication because we know the exact expression for the electric potential. We can ask: Why do we look for approximated expressions when we know the exact one?
The answer is that the exact expression is actually not so exact as we thought. Indeed, we can see that when we write the power expansion for \(1/r_+\) and \(1/r_-\), and substitute them in the expression for the potential, there is cancellation of several terms. This means that the net contribution of each individual charge to the potential of the dipole, is in reality less (or more, depending on whether the term to be canceled has positive or negative sign in the power expansion of the potential of the individual charge) than the potential of such a charge when it is alone. Therefore, what we actually do in the power expansion is to eliminate all the irrelevant information. After all of the cancellations, the remnant expression for the potential is truly exact, without superfluous information.
The only possible drawback is that the power expansion is valid only for distances larger than the separation between the charges in the dipole. So, we have an exact expression for the potential, which is valid only in certain region, and in addition, such expression has no analytic form but is a series. This drawback is offset by the fact that the dominant term is very often all what we need and, in addition, the dominant term is simpler than the original expression in terms of the potential of the two charges, while containing the more relevant information about the dipole potential.
An additional advantage of the expansion of the potential in powers of \(d/r\), is that it allows to introduce a theoretical particle which is called pure dipole. The potential of a pure dipole is more suitable for calculations and physical understanding.
Pure dipole and physical dipole
If we let the separation \(d\) between the charges tend to zero and at the same time let the charge \(q\) tend to infinity, while keeping constant the product \(p=qd\), then we can see that the expansion of the potential of the electric dipole in powers of \(d/r\), reduces to the expression
\[\Phi(r,\theta)=\frac{1}{4\pi\epsilon_0}\frac{p\cos\theta}{r^2}=\frac{1}{4\pi\epsilon_0}\frac{\vec{p}\cdot\hat{r}}{r^2}\]
The electric dipole obtained by this process of letting \(d\) go to zero and \(q\) go to infinity while keeping constant the product \(p=qd\), is called pure dipole. A pure dipole, is effectively a point particle with zero electric charge and nonzero moment of dipole \(\vec{p}\).![]()
A pure dipole is of course a theoretical construct. Its potential at any point is exactly the dominant term in the expansion in powers of \(d/r\) of the true electric dipole. In this context, the original dipole is called physical dipole to distinguish it from the theoretical pure dipole.
It is important to understand that the potential of the pure dipole is just an approximation to the potential of the physical dipole. Such approximation is valid for \(r\) much larger than \(d\).

Leave a comment