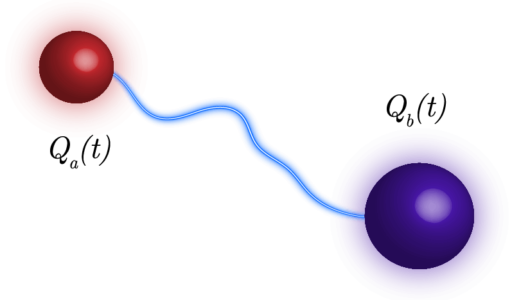
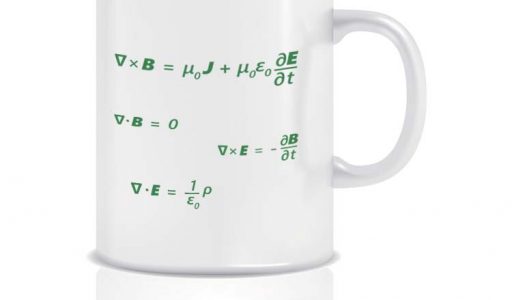In the present post, we calculate the dependence on time of the charges on two conducting spheres connected by a wire until reaching the electrostatic equilibrium.
We were taught that grounding a conductor (by connecting it to the ground with a wire) means fixing its electric potential to zero. That’s right, but what is the physical mechanism that fixes to zero the electric potential? Let’s see how grounding a conductor works in physical terms.
When I was a student, I remember they taught me that the method of images to solve the problem of finding the electrostatic potential outside a grounded conducting sphere in the presence of an external point charge is a kind of miracle. But in physics, there are not miracles. Here are the facts why the method works
The Maxwell equations are a set of four partial differential equations that describe the spatial and temporal behavior of electric \(\vec{E}\) and magnetic \(\vec{B}\) fields. The sources of time-independent electric and magnetic fields are the time-independent electric charge density \(\rho\) and the steady current density \(\vec{J}\) respectively.
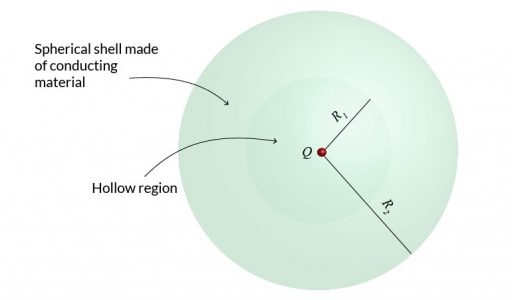
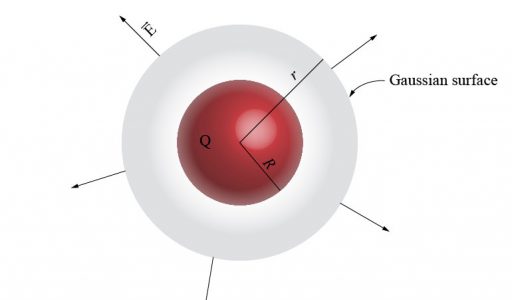
In the present post I will consider the problem of calculating the electric field due to a point charge \(Q\) surrounded by a conductor which has the form of a thick spherical shell
I will start with some conventional problems which are relatively easy, and after that, I will consider more advanced problems. I will show you how to solve some problems that seem to be challenging.
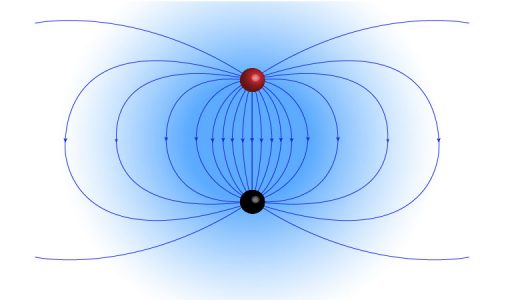
The concepts of electric dipole, potential of dipole, pure and physical dipoles are explained.